¿Cómo saber, estadísticamente, si tu gestor te aporta valor añadido? La respuesta: una simulación de Montecarlo y el ratio de Sharpe

Unas palabras iniciales: en este post quiero dejar claro que uno no sólo debe mirar la rentabilidad de una estrategia aleatoria, sino también otros aspectos, como la volatilidad de las estrategias. Es por esto que para determinar si un gestor es mejor que un mono, habría que mirar el ratio de Sharpe (rentabilidad/volatilidad) obtenidos a partir de una simulación de Montecarlo y no, como he visto en varios lugares, fijarse sólo en la rentabilidad.

He leído varias veces la idea de que un mono es mejor asesor financiero que cualquier gurú financiero. Esta idea parece que proviene del libro “Un paseo aleatorio por Wall Street” publicado por Burton Gordon Malkiel y en el que sugiere que la rentabilidad en la bolsa está más marcada por el azar que por las técnicas de inversión de la gestión activa de carteras. https://en.wikipedia.org/wiki/A_Random_Walk_Down_Wall_Street

Para el caso español, he encontrado en internet una referencia en donde, en vez de monos seleccionando empresas, se les pidió a 248 escolares entre 6 y 17 años que eligieran números al azar y luego esos números fueron utilizados para seleccionar empresas en donde invertir. Sucede que la rentabilidad media de estas decisiones aleatorias fue mejor que muchos fondos de inversión españoles. http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2720365

Tras esta introducción, vamos al grano, desde el punto de vista científico, ¿cómo contrasto la hipótesis de que una selección al azar es mejor que la sugerida por el asesor financiero que he contratado? La respuesta está en utilizar el método de Montecarlo para conocer la rentabilidad y la volatilidad media  de estrategias al azar (como realizadas por un mono), así como los valores extremadamente atípicos de este tipo de estrategias, a los que podríamos decir que es muy poco probable que sean generados por el azar.

Es decir, la idea es fijarse en la rentabilidad (o mejor en el ratio rentabilidad/volatilidad) obtenida por el asesor financiero en el último año y compararla con la distribución de rentabilidades de varias estrategias de compra/venta generadas aleatoriamente para el mismo periodo de tiempo (por cierto, esto es una simulación de Montecarlo https://es.wikipedia.org/wiki/M%C3%A9todo_de_Montecarlo). De esta forma sabría que: si la rentabilidad del gestor es más alta que la obtenida por el 95% de mis estrategias aleatorias, muy probablemente, el gestor me esté aportando valor añadido. Aunque aquí yo diría que más que fijarse solamente en la rentabilidad, habría que ver que tan arriesgadas han sido las estrategias aleatorias, es por eso que también compararé la desviación típica y el ratio rentabilidad/desviación típica (ratio de Sharpe). Así, es más recomendable fijarse en los fondos que tengan un mayor ratio de Sharpe (rentabilidad por unidad de volatilidad) que sólo fijarse en la rentabilidad. 

Utilizando STATA y el comando stockquote: bajaré los datos del IBEX desde enero de 2015 hasta principios de febrero de 2016. Asumiré que un inversor decide invertir en un ETF (fondo cotizado en bolsa) que replica el IBEX y que toma una decisión de compra o venta semanalmente (todos los miércoles por las mañanas, es decir, sin conocer aún el cierre del día). Hago esto porque generalmente el benchmark a batir por los fondos de inversión suele ser el propio IBEX.

Mi simulación de Montecarlo tirará una moneda cada miércoles entre 01/2015 y 02/2016  (distribución binomial con probabilidad 50/50) y decidirá comprar si sale cara (=1) y vender si sale cruz (=0).  Luego calcularé la rentabilidad media y la desviación típica de esta estrategia aleatoria. Este proceso lo repetiré 50mil veces, por lo que tendré 50mil rentabilidades y 50mil desviaciones típicas. Con estos datos ordenaré de menor a mayor las rentabilidades y desviaciones típicas y veré cuantas veces han ocurrido de las 50mil (esto es un histograma). Con este histograma en manos, podré decidir si la gestión de mi asesor es parecida o no a una estrategia aleatoria.

Antes de empezar, unos datos descriptivos del desempeño del IBEX en el periodo enero/2015 – febrero/2016. La rentabilidad media diaria del periodo fue de -0,05% diario (asumiendo interés simple y 262 días laborables, una pérdida anual de -13%, efectivamente la pérdida acumulada llegaba al -16% a principios de febrero de este año) con una volatilidad de +/- 1,4pp.

Dicho esto, veamos qué resultados da nuestro experimento de ordenador. En el gráfico 1 presento la rentabilidad diaria obtenida por las estrategias aleatorias que sólo pueden ponerse largas y tienen prohibido ponerse cortas (es decir, no pueden apostar en contra del índice y ganar cuando el IBEX cae, para una explicación de esto de corto/largo http://www.rankia.com/blog/fernan2/364450-ponerse-corto-abrir-cortos-cerrar ). La rentabilidad media de estas estrategias fue de -0,025% (tabla 1), por lo que podríamos estar tentados a decir que fue mejor que la evolución del IBEX en el mismo periodo (-0,05%), pero si indagamos un poco más vemos que está dentro del rango de una desviación típica, así que podríamos decir, con franqueza, que una estrategia aleatoria que sólo se ponga larga puede reproducir la evolución del índice o, lo que es lo mismo, reproducir una gestión pasiva de la cartera.

Ahora, para responder a la pregunta de si nuestro gestor nos da más rentabilidad que la de un mono (la estrategia aleatoria) nuestro asesor nos tendría que mostrar una rentabilidad diaria mayor al 0,04% (gráfico 1 y tabla 1). Rentabilidad muy elevada, por cierto, pero también injusta, porque la estrategia aleatoria quizás fue más volátil para conseguir esa rentabilidad. Así que, para ser más justos, yo elegiría un gestor que tenga un ratio rentabilidad/desviación típica mayor al 0,04 (este número lo obtengo de la tabla 2 y es el percentil 95 del ratio de sharpe de la estrategia aleatoria). O sea que si mi gestor me dice que tuvo una rentabilidad de 0,01% en ese periodo y veo que en sus reportes mensuales su desviación típica fue de 0,25pp, me seguiría quedando con él aunque sé que su rentabilidad está lejos de lo que, en media, me daría un estrategia aleatoria, aunque esta última también sería mucho más volátil y con los reportes mensuales no sería capaz de mantener el estrés de esa volatilidad.

Gráfico 1: Histogramas de rentabilidad diaria en % de las estrategias aleatorias que sólo pueden ponerse largas.

Tabla 1. Descriptivos de la rentabilidad diaria de las estrategias aleatorias que solo pueden ponerse largas

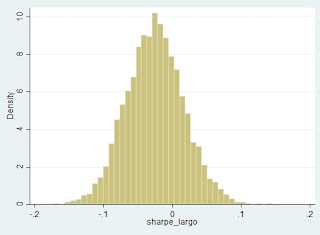
Gráfico 2: Distribución del ratio de Sharpe (rentabilidad/volatilidad) de las estrategias aleatorias que sólo se pueden poner largas

Tabla 2: Estadísticos descriptivos del ratio de Sharpe para estrategias aleatorias que sólo se pueden poner largas

Para el caso de las estrategias aleatorias que pueden colocarse cortas (apostar en contra del IBEX), la rentabilidad media es de 0% (mucho mejor que la pérdida media del IBEX en ese periodo y también mejor que la de la estrategia aleatoria que sólo puede ponerse larga). Su ratio rentabilidad/volatilidad es incluso mejor que la de las estrategias que sólo pueden ponerse largas (0 frente al -0.025 de la estrategia aleatoria larga). Es decir, en este caso, a la rentabilidad de 0,01% de mi asesor financiero tendré que pedirle que su volatilidad haya sido de solo 0.10pp (frente al 0.25pp que le pedía frente a la estrategia anterior).

Gráfico 3: Histogramas de rentabilidad diaria en % de las estrategias aleatorias que pueden ponerse cortas (apostar en contra del IBEX)

Tabla 3. Descriptivos de la rentabilidad diaria de las estrategias aleatorias que pueden ponerse cortas (apostar en contra del IBEX)

Gráfico 4: Distribución del ratio de Sharpe (rentabilidad/volatilidad) de las estrategias aleatorias que pueden ponerse cortas (apostar en contra del IBEX)

Tabla 4: Estadísticos descriptivos del ratio de Sharpe (rentabilidad/volatilidad) para estrategias aleatorias que pueden ponerse cortas (apostar en contra del IBEX)

Para concluir, si quiero saber si un gestor lo está haciendo realmente bien lo tengo que comparar contra algún índice, pero no sólo en cuanto a rentabilidad, sino también en relación a volatilidad (prefiero que me dé la mayor rentabilidad con la menor volatilidad posible). Una simulación de Montecarlo me puede ayudar a discernir si alguien lo está haciendo mejor que un apostador de casino, pero si no puedo realizar esta simulación, la opción que tengo es ver la evolución de algún índice y su volatilidad en ese periodo, calcular el ratio de Sharpe y compararlo con el desempeño del gestor.

Aquí el código de Stata utilizado 

//////////////////////////////////////////////
// Autor: Diego José Torres Torres twitter @diego_torres
// Las opiniones reflejadas en este post no reflejan la posición oficial de la institución a la cual pertenezco, son exclusivamente mías y fuera del ámbito laboral
// ¿Cómo saber si un gestor de activos está generando valor añadido y cuánto?
// o ¿Es mi gestor un mono? y ¿cómo identificarlo?
//////////////////////////////////////////////

************************************************************************************
* Paso 1: Descargar e instalar el comando stockquote para poder bajarme los datos de las acciones
findit stockquote  // buscarlo y luego seguir los pasos para instalarlo
************************************************************************************
* Paso 2:  Descargar los datos diarios del ibex desde enero de 2015 hasta FEBRERO de 2016
stockquote ^IBEX, fm(1) fd(2) fy(2015) lm(02) ld(3) ly(2016) frequency(d)
save "C:\Users\qtorres\Programs\Z Personal\Stata\MonteCarlo\basedatos_Ibex.dta", replace
**
use "C:\Users\qtorres\Programs\Z Personal\Stata\MonteCarlo\basedatos_Ibex.dta", clear
************************************************************************************
* Paso 3: Crear una variable de fecha y definir que es una serie de tiempo (como los días son laborables crearé una fecha ficticia sin saltos aparte de la real)
gen daterec = date(date, "YMD") // Fecha real
format daterec %td
gen t =_n // fecha ficticia para los cálculos de series de tiempo
tsset t

************************************************************************************
* Paso 4 Calculo la variación diaria (en %) del IBEX
gen ibex_daily = (adjclose-L.adjclose)/L.adjclose *100

************************************************************************************
* Paso 5: Voy a asumir que la decisión de inversión se realiza semanalmente (los miércoles a primera hora del día (o lo que es lo mismo, los martes al final del día, es decir, sin saber el cierre del día)).
* Por lo que creo la variable que identifica los días miércoles
gen diasemana=dow(daterec) // 0=domingo, con lo cual 3=miércoles
gen miercoles = diasemana==3

************************************************************************************
* Paso 6: Identificar en la base el primer miércoles para luego calcular desde ese día:
** 1- el desempeño de la bolsa
** 2- el drawdown (pérdida máxima)
** 6.1- bucle para encontrar el primer miércoles
global i=1
while miercoles[$i] == 0  {
global  i=$i + 1
}

** 6.2- Calculo el desempeño del ibex (gestión pasiva de la cartera)
local escalar = adjclose[$i-1]
gen desempenho_ibex = adjclose[_n] / `escalar' * 100 if _n >= $i
replace desempenho_ibex = 100 if _n == $i-1

** 6.3 Reemplazo con valores perdidos las variaciones diarias del IBEX previas al incio de la gestión (primer miércoles)
replace ibex_daily=. if desempenho_ibex==. | _n <$i // también tengo que eliminar la variación del día base porque ese dato ya era conocido
** Calculo el DrawDown
gen ibex_drawdown=.
global N = _N
set more off
forvalues n = 2/$N {
// DrawDown Modelo
qui su desempenho_ibex if _n<=`n'
replace ibex_drawdown = desempenho_ibex - r(max) if _n == `n'
}             

//////////////////////////////////////////////////////////////////////////////////////////////////
// DEFINIENDO EL ALGORITMO DE MONTECARLO PARA OBSERVAR LA DISTRIBUCIÓN DE RENTABILIDADES, RIESGO, PÉRDIDA MÁXIMA
// RATIO DE SHARPE PARA UNA SERIE DE MONOS QUE TRABAJAN PARA MI
//////////////////////////////////////////////////////////////////////////////////////////////////

global nmc = 10000 // cantidad de monos que trabajarán para mi (o número de replicaciones para el montecarlo)

capture program drop estrategia_aleatoria // para borrar un programa definido

***** Se inicia la definición del programa
program estrategia_aleatoria, rclass

tempname sim

// Defino el nombre de la base en la cual haré las replicaciones  y las variables que voy a guardar en la base "results"
postfile `sim' r_ibex se_ibex r_acumulado_ibex drawdown_ibex  r_aleatoria_corto r_aleatoria_largo se_aleatoria_corto se_aleatoria_largo  r_acumulado_corto r_acumulado_largo drawdown_aleatorio_corto drawdown_aleatorio_largo  using results, replace
quietly {
forvalues i = 1/$nmc {   
noisily dis "Iteración: " `i'
************************************************************************************
* Paso 7: Gestión activa realizada al azar: realizo una compra (= 1) o en todo caso una venta (= 0) dependiendo del valor de una variable aleatoria binomial (como por ejemplo tirar una moneda).
gen compra_aleatoria=.
replace compra_aleatoria = rbinomial(1,0.5) if miercoles==1 // Random strategy

// Mantengo la posición toda la semana
global N = _N
set more off
forvalues n = 2/$N {
replace compra_aleatoria = compra_aleatoria[`n' - 1] if compra_aleatoria==. & _n==`n'

************************************************************************************
* Paso 8: Calcular el desempeño y el drawdown de esta estrategia aleatoria (sin cortos, sólo poniendome largo)
gen desempenho_aleatorio_largo = 100 if _n==1
global N = _N
set more off
forvalues n = 2/$N {
replace desempenho_aleatorio_largo = 100 if compra_aleatoria==. // porque solo hay perdidos al inicio de la base
replace desempenho_aleatorio_largo = desempenho_aleatorio_largo[`n' - 1]*(1+ibex_daily[`n']/100) if compra_aleatoria==1 & _n==`n' & ibex_daily[`n']!=.
replace desempenho_aleatorio_largo = desempenho_aleatorio_largo[`n' - 1] if compra_aleatoria==0 & _n==`n'
}
* Reemplazo con valores perdidos los días previos al inicio de la estrategia
replace desempenho_aleatorio_largo=. if desempenho_ibex==.

* calculando el Drawdown
gen largo_drawdown=.
global N = _N
set more off
forvalues n = 2/$N {
// DrawDown Modelo
qui su desempenho_aleatorio_largo if _n<=`n'
replace largo_drawdown = desempenho_aleatorio_largo - r(max) if _n == `n'
}             

* calculando la rentabilidad diaria
gen largo_daily = (desempenho_aleatorio_largo-L.desempenho_aleatorio_largo)/L.desempenho_aleatorio_largo *100

************************************************************************************
* Paso 9: Calcular el desempeño de esta estrategia aleatoria pero poniéndose cortos
gen desempenho_aleatorio_corto = 100 if _n==1
global N = _N
set more off
forvalues n = 2/$N {
replace desempenho_aleatorio_corto = 100 if compra_aleatoria==. // porque solo hay perdidos al inicio de la base
replace desempenho_aleatorio_corto = desempenho_aleatorio_corto[`n' - 1]*(1+ibex_daily[`n']/100) if compra_aleatoria==1 & _n==`n' & ibex_daily[`n']!=.
replace desempenho_aleatorio_corto = desempenho_aleatorio_corto[`n' - 1]*(1-ibex_daily[`n']/100)  if compra_aleatoria==0 & _n==`n'
}
replace desempenho_aleatorio_corto=. if desempenho_ibex==.

* calculando el Drawdown
gen corto_drawdown=.
global N = _N
set more off
forvalues n = 2/$N {
// DrawDown Modelo
qui su desempenho_aleatorio_corto if _n<=`n'
replace corto_drawdown = desempenho_aleatorio_corto - r(max) if _n == `n'
}             
* calculando la rentabilidad diaria
gen corto_daily = (desempenho_aleatorio_corto-L.desempenho_aleatorio_corto)/L.desempenho_aleatorio_corto *100
************************************************************************************
* AQUÍ ME VOY A GRABAR LA MEDIA, LA DESVIACIÓN TÍPICA, EL MÁXIMO DRAWDOWN Y LA RENTABILIDAD ACUMULADA DE CADA UNO DE MIS MONITOS (DE LOS QUE SE PONEN CORTOS Y LARGOS Y LOS QUE SE PONEN SOLO LARGOS)
************************************************************************************
** Rentabilidad, desviación típica y último valor
** Las variables del monito que se pone sólo largo
su largo_daily  // para ver las variables que quedan en memoria (return list)
scalar  r_aleatoria_largo = r(mean)
scalar se_aleatoria_largo =  r(sd)
scalar r_acumulado_largo = desempenho_aleatorio_largo[_N]
su largo_drawdown
scalar drawdown_aleatorio_largo = r(min)

** Las variables del monito que se pone sólo largo y corto
su corto_daily  // para ver las variables que quedan en memoria (return list)
scalar  r_aleatoria_corto = r(mean)
scalar se_aleatoria_corto =  r(sd)
su corto_drawdown
scalar drawdown_aleatorio_corto = r(min)
** También el del Ibex
su ibex_daily
scalar  r_ibex = r(mean)
scalar se_ibex =  r(sd)
scalar r_acumulado_ibex = desempenho_ibex[_N]
su ibex_drawdown
scalar drawdown_ibex = r(min)

** Pego los variables de la base actual (sim) en la nueva base (results) NOTA: TIENE QUE SER EN EL MISMO ORDEN DEFINIDO MÁS ARRIBA
post `sim' (r_ibex) (se_ibex) (r_acumulado_ibex) (drawdown_ibex)  (r_aleatoria_corto) (r_aleatoria_largo) (se_aleatoria_corto) (se_aleatoria_largo)  (r_acumulado_corto) (r_acumulado_largo) (drawdown_aleatorio_corto) (drawdown_aleatorio_largo)

** Elimino las variables que se fueron creando en cada bucle                                   
drop compra_aleatoria desempenho_aleatorio_largo largo_drawdown largo_daily desempenho_aleatorio_corto corto_drawdown corto_daily
scalar drop _all
}
}
postclose `sim'
end


/////////////////////////////////////////////////////////////////////////////////////////////////
// aquí llamo al programa que definí más arriba (estrategia_aleatoria )
//////////////////////////////////////////////////////////////////////////////////////////////////

estrategia_aleatoria // ejecuto el programa definido en la línea de código 74

* Abro la base que creó el programa ejecutado
use results, clear

* Veo el histograma de cortos y largos
twoway (histogram r_aleatoria_corto  , color(green)) ///
(histogram r_aleatoria_largo , fcolor(none) lcolor(black)), legend(order(1 "Rentabilidad Corto" 2 "Rentabilidad Largo" ))


** Calculo los quantiles 5 y 95, así sabré qué rentabilidad es demasiado alta (o demasiado baja) para suponer que el gestor es un mono
su r_aleatoria_largo , d
scalar largo_per5=r(p5)
scalar largo_per95=r(p95)

su r_aleatoria_corto , d
scalar corto_per5=r(p5)
scalar corto_per95=r(p95)
scalar list

** generando ratio de sharpe
gen sharpe_corto = r_aleatoria_corto /  se_aleatoria_corto
hist sharpe_corto

gen sharpe_largo = r_aleatoria_largo /  se_aleatoria_largo
hist sharpe_largo

gen sharpe_ibex = r_ibex / se_ibex

** Histogramas de Sharpe
twoway (histogram sharpe_corto  , color(green)) ///
(histogram sharpe_largo , fcolor(none) lcolor(black)), legend(order(1 "Sharpe Corto" 2 "Sharpe Largo" ))


** DrawDown
twoway (histogram drawdown_aleatorio_corto  , color(green)) ///
 (histogram drawdown_aleatorio_largo , fcolor(none) lcolor(black)), legend(order(1 "Drawdown Corto" 2 "Drawdown Largo" ))


save "C:\Users\qtorres\Programs\Z Personal\Stata\MonteCarlo\results_Ibex.dta", replace